ヘロンの公式とは、三角形の面積算出時に使う公式です。
この記事では、ヘロンの公式の内容や計算方法、どこで使うかを解説します。
ヘロンの公式とは?
ヘロンの公式は三角形の面積算出時に使う公式です。
三角形は底辺×高さ÷2で算出する計算式を習いましたよね?
現場の形状は面積が簡単に求まる形状ばかりではありませんが、複雑な形も必ず三角形に分割することができます。
そこで、三辺の長さから面積が算出できるヘロンの公式が活用されています。
それぞれの三角形の高さを測れば良いのでは?と思うかもしれませんが、それでは手間が増えすぎてしまうため、避けられています。
それでは、ヘロンの公式について見ていきましょう。
下の図のように辺の長さがa、b、cである三角形ができたとき、
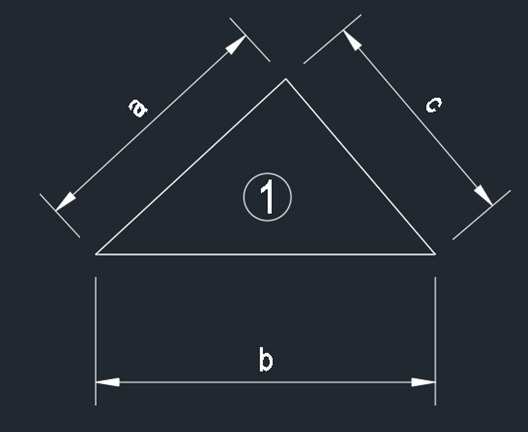
s=(a+b+c)÷2
とおくと、
面積A=√(s(s-a)(s-b)(s-c))となります。
これがヘロンの公式です。
ヘロンの公式を用いた計算方法
計算方法を具体に見ていきましょう。
まず、三角形のそれぞれの辺の長さを算定します。

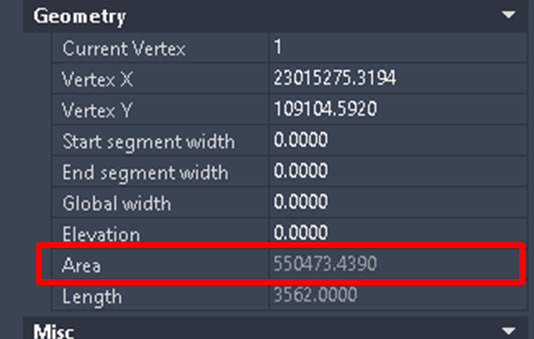
例題の三角形の各辺の長さはa=1,113mm、b=1,459mm、c=990mmとなりました。
ヘロンの公式に当てはめると・・・・
s=(a+b+c)÷2 =(1,113 + 1,459 + 990)÷2=1,781 (mm)となり、
面積A
=√(s(s-a)(s-b)(s-c))
=√(1781×668×322×791)
=550473.439
と求まります。
CAD上で求めた面積とも合致しますね。
このヘロンの公式が便利なのは、どのような三角形の形でも面積が算出できること。
何度も計算を行う場合は、エクセルでフォーマットを作成するのがお勧めです。
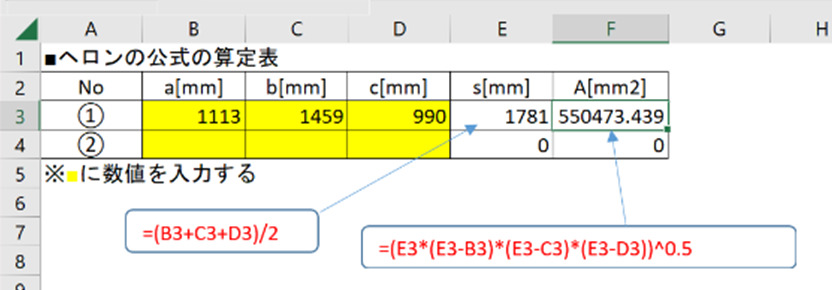
図 ヘロンの公式のフォーマット例
ヘロンの公式はどこで使う?
今はCADソフトもありますので、実は面積を簡単に算出することができます。
ただし、傾斜している場所(堤防の法面など)については、面積を平面図上から算出することができません。
そのため、土木現場では、堤防の法面など勾配を持った範囲の面積を算出する場合に用いられています。
近年、3次元CADによる体積や面積の自動算出機能が用いられるようになってきていますので、技術的には法面の面積もソフト上で計算できるようになりました。
そのため、ヘロンの公式も使わなくなってくるかもしれません。
ただし!
ソフトによるCAD求積は、単位や縮尺設定ミスにより全く異なる面積を出力することがありますので、概略チェックは忘れずに!