断面二次モーメントとは、曲げモーメントに対し部材がどれほど耐えることができるのかを部材の断面形状から判断できる値。
この記事では、断面二次モーメントの意味や公式、計算事例について解説します。
断面二次モーメントとは
部材は外力に応じて、伸びたり縮んだり曲がったりしますが、この伸び縮みや曲げに対する部材の強さは、部材の物性はもちろん、部材の形状によっても異なります。
ここで曲げについて注目した際に重要となるのが「断面二次モーメント」というキーワード。
断面二次モーメントとは、曲げモーメントに対し部材がどれほど耐えることができるのかを部材の断面形状から判断できる値となります。
つまりは変形しにくさですね。
断面二次モーメントは大きいほど変形しにくく、小さいほど変形しやすいことを意味します。
同じような意味を持つ「断面係数」という言葉がありますが、断面係数は曲げた際の応力の強さを表しますので注意しましょう。
たわみとの関係
断面二次モーメント:Iから梁のたわみ量:σも計算することでき、下の図のように片持ち梁の先端に荷重:Wが梁に付加されたときのたわみ量は以下の通りとなります。
σ=WL3/3EI
・L:梁の長さ
・E:ヤング率
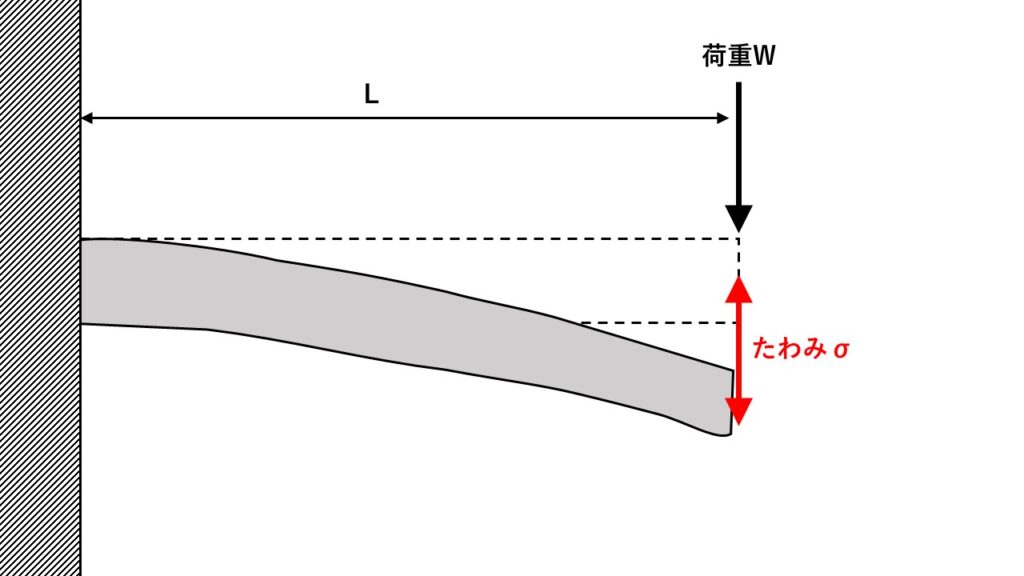
図1.片持ちはりのたわみ
実際は梁の種類や負荷のかけ方によって、公式の係数が若干変わるので注意ください。
この公式を考察すると、分子にある荷重や梁の長さが大きくなるとたわみも大きくなり、分母にあるヤング率や断面二次モーメントが大きくなると、たわみが小さくなることが分かります。
つまり冒頭でも説明した通り、断面二次モーメントが大きいほど梁は変形しにくく
小さいほど変形しやすいことが公式から分かります。
断面二次モーメントの公式(主要な形状)
単純な梁に曲げモーメントが作用した場合、内側では圧縮応力が、外側では引張応力が作用するが、圧縮応力と引張応力が作用しない中立地点(軸)が存在します。
ここで、断面二次モーメントの至極簡単な定義として、「断面積×中立軸からの距離の2乗」があります。
導出は省略しますが、主要な断面形状での断面二次モーメント一覧を紹介しますのでご参考下さい。
(1)正方形
I=a4/12
(2)長方形
I=bh312
(3)丸
I=πd4/12
(4)H形鋼(フィレット部は考慮せず)
I=(BH3+bh3)/12
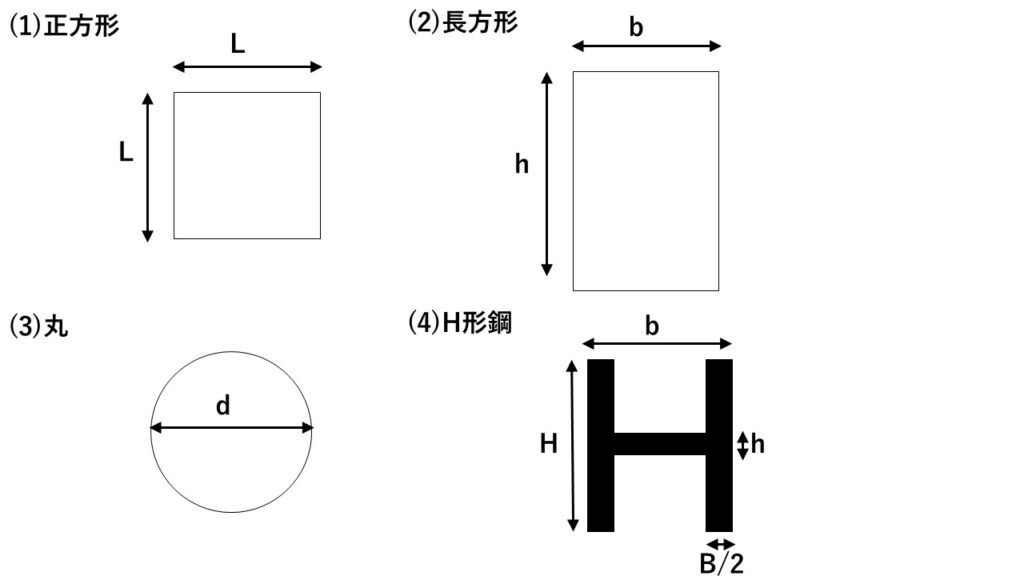
図2.断面形状
断面二次モーメントの計算例(H形鋼)
ここで実例として以下の場合の断面二次モーメントとたわみを計算してみましょう。
条件として、長さ1mのH形鋼が片持ち梁になっており、先端に荷重W(=100N)が作用しており、H形鋼としては、広巾の100×100×6×8を使用しています。
まず断面二次モーメントを算出します。
I=(BH3+bh3)/12より
I={(8×2×(100)3+100×(6)3)}/12
=1,335,133mm4
次にたわみを求めます。
たわみの公式は次の通りです。
σ=WL3/3EI
ここでW=100N、L=1m(=1,000mm)、H形鋼のヤング率Eは205,000N/mm2であり
断面二次モーメントも代入すると、σ=0.122mmとなります。
100Nの力を加えても0.12mm程度しかたわまないことからもH形鋼が建築資材として重宝されている理由が分かりますね。
断面二次モーメントは便利な考え方ですので、ぜひマスターしましょう。